#308 7-Segment Combinational Logic
Dust off some combinational logic methods and build a 8421-BCD to 7-segment LED driver with 7400 series logic.

Here’s a quick video of it in action:
Notes
Ben Eater published a fantastic video/tutorial on designing a 7-segment hex decoder as an adjunct to his Building an 8-bit breadboard computer quest.
The first take-away is of course:
that’s an awful lot of work just to drive a 7-segment display .. lucky we don’t have to do that these days!
My next thought was: OK, now make one too;-) I have vague memories of learning digital logic at uni, but I don’t recall that we ever did anything particularly ambitious with real hardware.
Constraints and Variations
Based on what’s in my part drawers, this is my goal:
- build a driver to take a nibble (4 binary inputs) and display the corresponding digits 0-9
- to simply things, I’ll call the inputs 0xA-0xF “undefined” and the output is “don’t care”
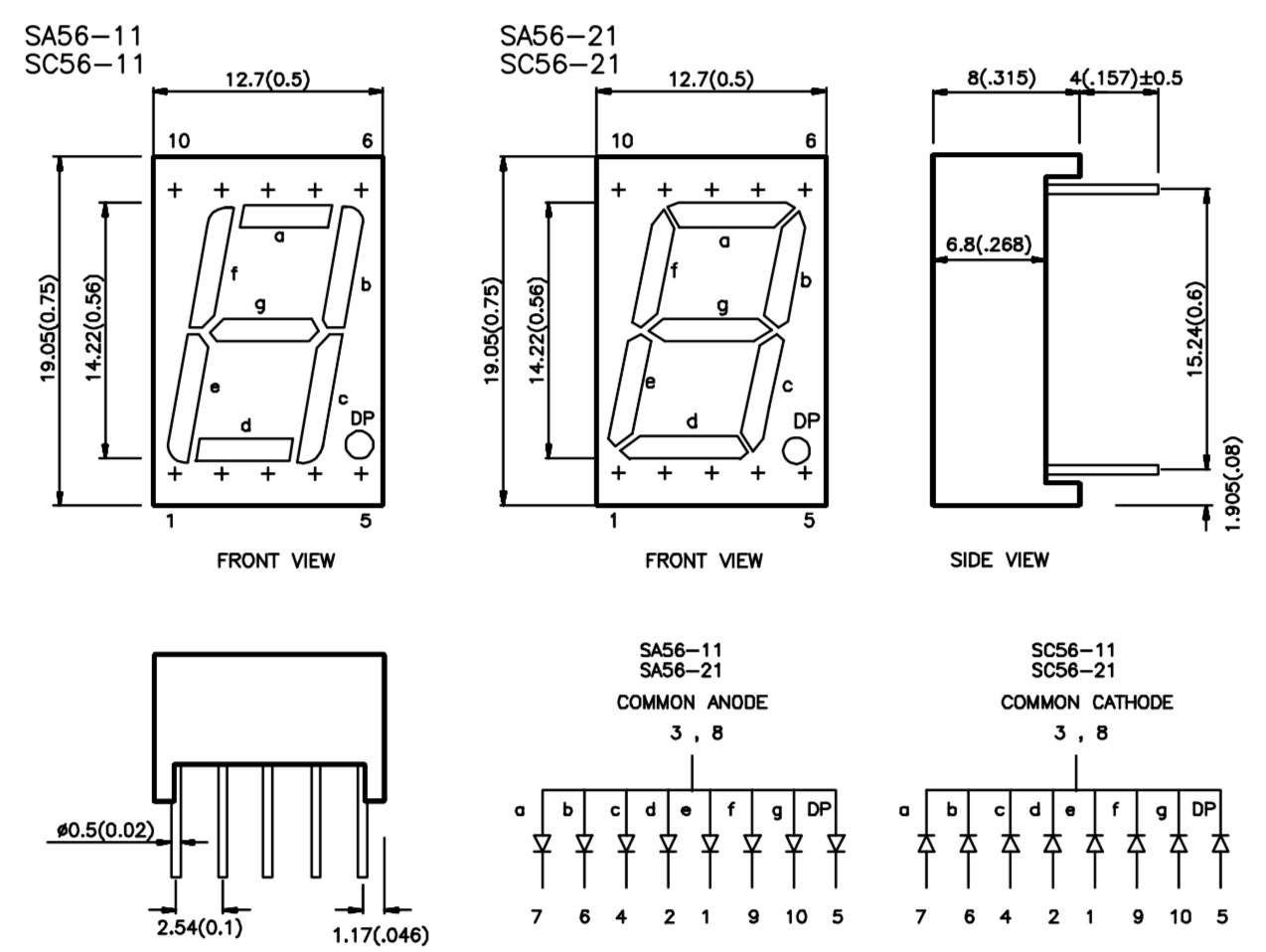
- on a common-cathode 7-segment LED display (SC56-11)
- using 7400 series logic. Any or all of the following gates: inverter, 2-input NAND, 2-input NOR, 2-input OR, 2-input XOR.
Ben demonstrated a circuit with a common-anode display and using only NOT, AND, OR gates. That’s good - stops me from simply copying the circuit. I’ll have to go back to first principles!
Input and Output
I’m using the a,b,c,d,e,f,g,dp naming convention for the LED pins, and I’ll call the 4 inputs w,x,y,z.
So the input to output transformation required for the digits 0-9 is as follows:
| Decimal Digit | w | x | y | z | a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| (don’t care) | 1 | 0 | 1 | 0 | X | X | X | X | X | X | X |
| (don’t care) | 1 | 0 | 1 | 1 | X | X | X | X | X | X | X |
| (don’t care) | 1 | 1 | 0 | 0 | X | X | X | X | X | X | X |
| (don’t care) | 1 | 1 | 0 | 1 | X | X | X | X | X | X | X |
| (don’t care) | 1 | 1 | 1 | 0 | X | X | X | X | X | X | X |
| (don’t care) | 1 | 1 | 1 | 1 | X | X | X | X | X | X | X |
NB: I’m calling the inputs 0xA-0xF “undefined”. This approach could of course be extended for hexadecimal display, but I’m sticking to decimal for now.
Deriving the Transformation Functions
With 4 inputs and 7 outputs, the truth table is large enough to defy just staring at it and hoping the answer will pop out. And a trial-and-error/brute force approach is likely to get very tedious, very quickly. So perhaps time to dust off my crusty knowledge of Boolean Algebra, Combinational logic, Karnaugh Maps and methods for simplification of boolean functions. I even opened my 1979 edition of Digital Logic & Computer Design for the first time in years (I had to find it first).
So bearing that all in mind.. what follows is my analysis and derivation of the transformation functions I’ll build into a circuit. I managed to get something that works, but I certainly don’t guarantee it is the simplest solution possible.
Some useful identities:
x.y == (x' + y')' i.e. AND(x, y) == NOR(NOT(x), NOT(y))
x + y == (x'y')' i.e. OR(x, y) == NAND(NOT(x), NOT(y))
x'y + xy' == XOR(x,y)
Transformation Functions
These are the final tranformation functions for the circuit design. I’ve dropped the algebraic notation and expressed as a combination of NOT, NOR, NAND, XOR functions (gates) I have available.
Derivations and notes follow.
| Function | Equivalent Gate Logic |
|---|---|
| f(a) | NAND(NOR(w, y), XOR(x, z)) |
| f(b) | NAND(NOR(w, NOT(x)), XOR(y, z)) |
| f(c) | NAND(NOR(w, x), NOR(NOT(y), z)) |
| f(d) | OR(NOR(z, NOR(w, y)), OR(NOR(NOT(x), OR(y, NOT(z))), NOR(x, NOR(y, NOT(z))))) |
| f(e) | OR(NOR(x, z), NOR(NOT(y), z)) |
| f(f) | OR(w, OR(NOR(y, NOR(x, NOT(z))), NOR(NOT(x), z))) |
| f(g) | NAND(NOT(w), OR(NOR(x, y), NOR(NOT(x), OR(NOT(y), NOT(z))))) |
f(a)
By inspection, a is only low in two cases, so the simplest starting point is probably f(a)' as a sum of minterms:
f(a)' = m1 + m4
= w'x'y'z + w'xy'z'
= w'y'(x'z + xz')
= (w + y)'(x'z + xz')
= AND(NOR(w, y), XOR(x, z))
So f(a) = NAND(NOR(w, y), XOR(x, z))
f(b)
Again by inspection, b is only low in two cases, so the simplest starting point is probably f(b)' as a sum of minterms:
f(b)' = m5 + m6
= w'xy'z + w'xyz'
= w'x(y'z + yz')
= (w + x')'(y'z + yz')
= AND(NOR(w, NOT(x)), XOR(y, z))
So f(b) = NAND(NOR(w, NOT(x)), XOR(y, z))
f(c)
Again by inspection, c is only low in one case, so the simplest starting point is f(c)' as a sum of minterms:
f(c)' = m2
= w'x'yz'
= (w + x)'(y' + z)'
= AND(NOR(w, x), NOR(NOT(y), z))
So f(c) = NAND(NOR(w, x), NOR(z, NOT(y)))
f(d)
d is low in four cases, so the inverse f(d)' can be expressed as a sum of 4 minterms: m1 + m4 + m7 + m9.
The Karnaugh Map technique is probably easiest here:
| wx \ yz | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 0 | 1 | 1 |
| 01 | 0 | 1 | 0 | 1 |
| 11 | x | x | x | x |
| 10 | 1 | 0 | x | x |
By map inspection:
f(d) = yz' + wz' + xy'z + x'(y + z')
= z'(w + y) + x(y + z')' + x'(y + z')
= (z + (w + y)')' + (x' + (y + z'))' + (x + (y + z')')'
= OR(NOR(z, NOR(w, y)), OR(NOR(NOT(x), OR(y, NOT(z))), NOR(x, NOR(y, NOT(z)))))
f(e)
e is high in four cases, so can be expressed as a sum of 4 minterms: m0 + m2 + m6 + m8
The Karnaugh Map technique is probably easiest here:
| wx \ yz | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 0 | 0 | 1 |
| 01 | 0 | 0 | 0 | 1 |
| 11 | x | x | x | x |
| 10 | 1 | 0 | x | x |
By map inspection:
f(e) = x'z' + yz'
= (x + z)' + (y' + z)'
= OR(NOR(x, z), NOR(z, NOT(y)))
f(f)
f is low in four cases, so easiest to express the inverse f(f)' as a sum of 4 minterms: m1 + m2 + m3 + m7
The Karnaugh Map technique is probably easiest here:
| wx \ yz | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 0 | 0 | 0 |
| 01 | 1 | 1 | 0 | 1 |
| 11 | x | x | x | x |
| 10 | 1 | 1 | x | x |
By map inspection:
f(f) = w + xy' + y'z' + xz'
= w + y'(x + z') + xz'
= w + (y + (x + z')')' + (x' + z)'
= OR(w, NOR(y, NOR(x, NOT(z))), NOR(NOT(x), z))
= OR(w, OR(NOR(y, NOR(x, NOT(z))), NOR(z, NOT(x))))
f(g)
By inspection, g is only low in three cases, so the simplest starting point is probably f(g)' as a sum of minterms:
f(g)' = m0 + m1 + m7
= w'x'y'z' + w'x'y'z + w'xyz
= w'x'y'(z' + z) + w'xyz
= w'x'y' + w'xyz
= w'(x'y' + xyz)
= w'(x'y' + (x' + y' + z')')'
= AND(NOT(w), OR(NOR(x, y), NOR(NOT(x), OR(NOT(y), NOT(z)))))
So f(g) = NAND(NOT(w), OR(NOR(x, y), NOR(NOT(x), OR(NOT(y), NOT(z)))))
Construction
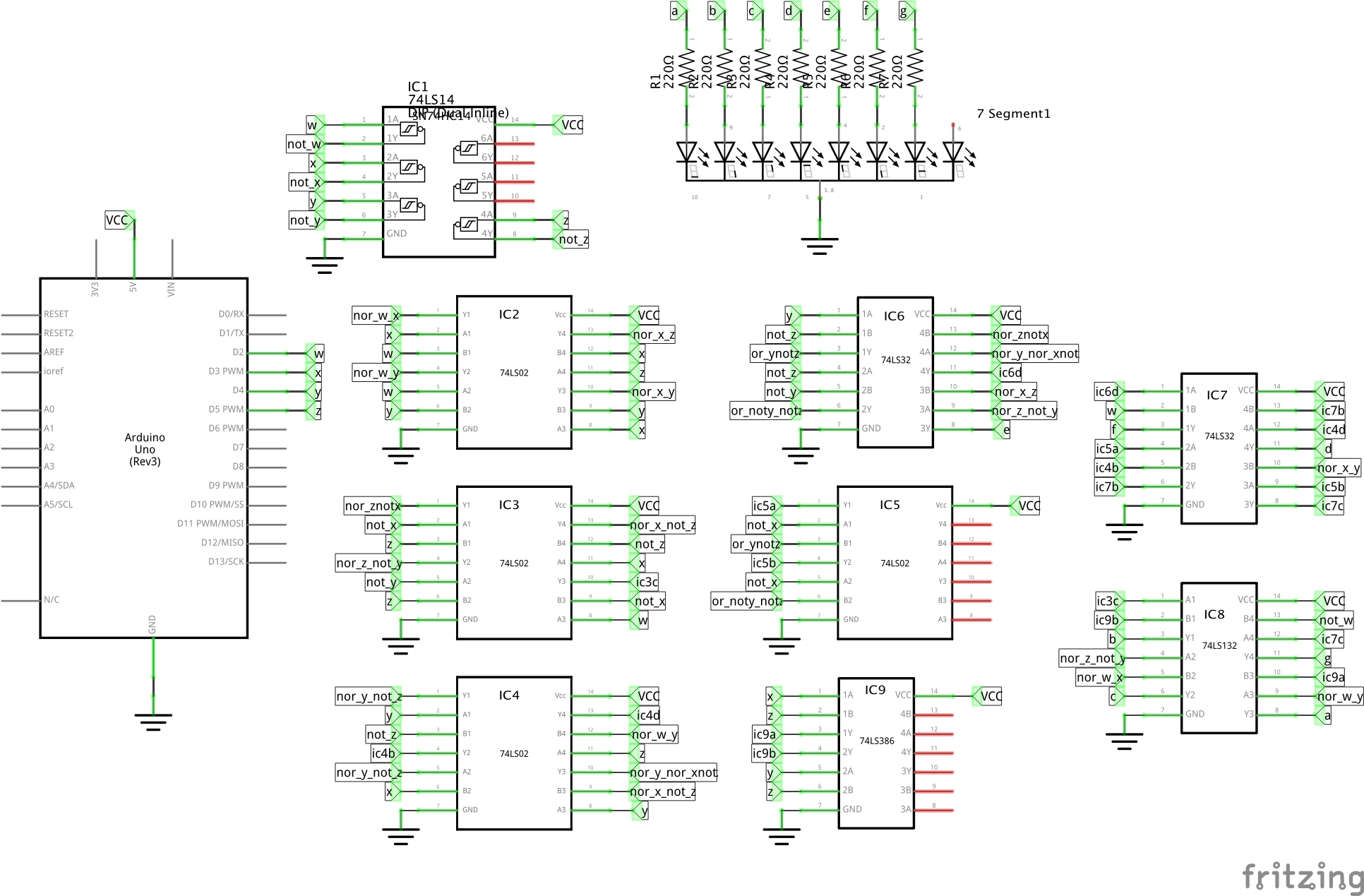
Distinct gates, after decomposition and sorting:
| Type | Function | Allocation | Mnemonic |
|---|---|---|---|
| NAND | NAND(NOR(w, NOT(x)), XOR(y, z)) # [ic3c,ic9b] | IC8a | b |
| NAND | NAND(NOR(w, x), NOR(z, NOT(y))) # [nor_w_x, nor_z_not_y] | IC8b | c |
| NAND | NAND(NOR(w, y), XOR(x, z)) # [nor_w_y, ic9a] | IC8c | a |
| NAND | NAND(NOT(w), OR(NOR(x, y), NOR(NOT(x), OR(NOT(y), NOT(z))))) # [not_w,ic7c] | IC8d | g |
| NOR | NOR(NOT(x), OR(NOT(y), NOT(z))) | IC5b | ic5b |
| NOR | NOR(NOT(x), OR(y, NOT(z))) # [not_x,or_ynotz] | IC5a | ic5a |
| NOR | NOR(z, NOT(x)) | IC3a | nor_znotx |
| NOR | NOR(z, NOT(y)) | IC3b | nor_z_not_y |
| NOR | NOR(w, NOT(x)) | IC3c | ic3c |
| NOR | NOR(w, x) | IC2a | nor_w_x |
| NOR | NOR(w, y) | IC2b | nor_w_y |
| NOR | NOR(x, NOR(y, NOT(z))) | IC4b | ic4b |
| NOR | NOR(x, NOT(z)) | IC3d | |
| NOR | NOR(x, y) | IC2c | nor_x_y |
| NOR | NOR(x, z) | IC2d | |
| NOR | NOR(y, NOR(x, NOT(z))) | IC4c | nor_y_nor_xnotz |
| NOR | NOR(y, NOT(z)) | IC4a | |
| NOR | NOR(z, NOR(w, y)) # [z,nor_w_y] | IC4d | ic4d |
| NOT | NOT(w) | IC1a | |
| NOT | NOT(x) | IC1b | |
| NOT | NOT(y) | IC1c | |
| NOT | NOT(z) | IC1d | |
| OR | OR(NOR(NOT(x), OR(y, NOT(z))), NOR(x, NOR(y, NOT(z)))) # [ic5a, ic4b] | IC7b | ic7b |
| OR | OR(NOR(x, y), NOR(NOT(x), OR(NOT(y), NOT(z)))) # [nor_x_y, ic5b] | IC7c | ic7c |
| OR | OR(NOR(x, z), NOR(z, NOT(y))) | IC6c | e |
| OR | OR(NOR(y, NOR(x, NOT(z))), NOR(z, NOT(x))) # [nor_y_nor_xnotz,nor_znotx] | IC6d | ic6d |
| OR | OR(NOR(z, NOR(w, y)), OR(NOR(NOT(x), OR(y, NOT(z))), NOR(x, NOR(y, NOT(z))))) # [ic4d,ic7b] | IC7d | d |
| OR | OR(NOT(y), NOT(z)) | IC6b | |
| OR | OR(w, OR(NOR(y, NOR(x, NOT(z))), NOR(z, NOT(x)))) | IC7a | f |
| OR | OR(y, NOT(z)) | IC6a | or_ynotz |
| XOR | XOR(x, z) | IC9a | ic9a |
| XOR | XOR(y, z) | IC9b | ic9b |
So IC requirements:
- 4 x NAND, so use 1 x 74LS132
- 14 x NOR, so use 4 x 74LS02
- 4 x NOT, so use 1 x 74LS14
- 8 x OR, so use 2 x 74LS32
- 2 x XOR, so used 1 x 74LS386
Power Consumption when tested on the breadboard with VCC=5V
- maximum total current is less than 50mA
- maximum current for any of the input lines (w,x,y,z) is less than 2mA
So therefore, quite safe to power and drive with an Arduino Uno. Just checking!
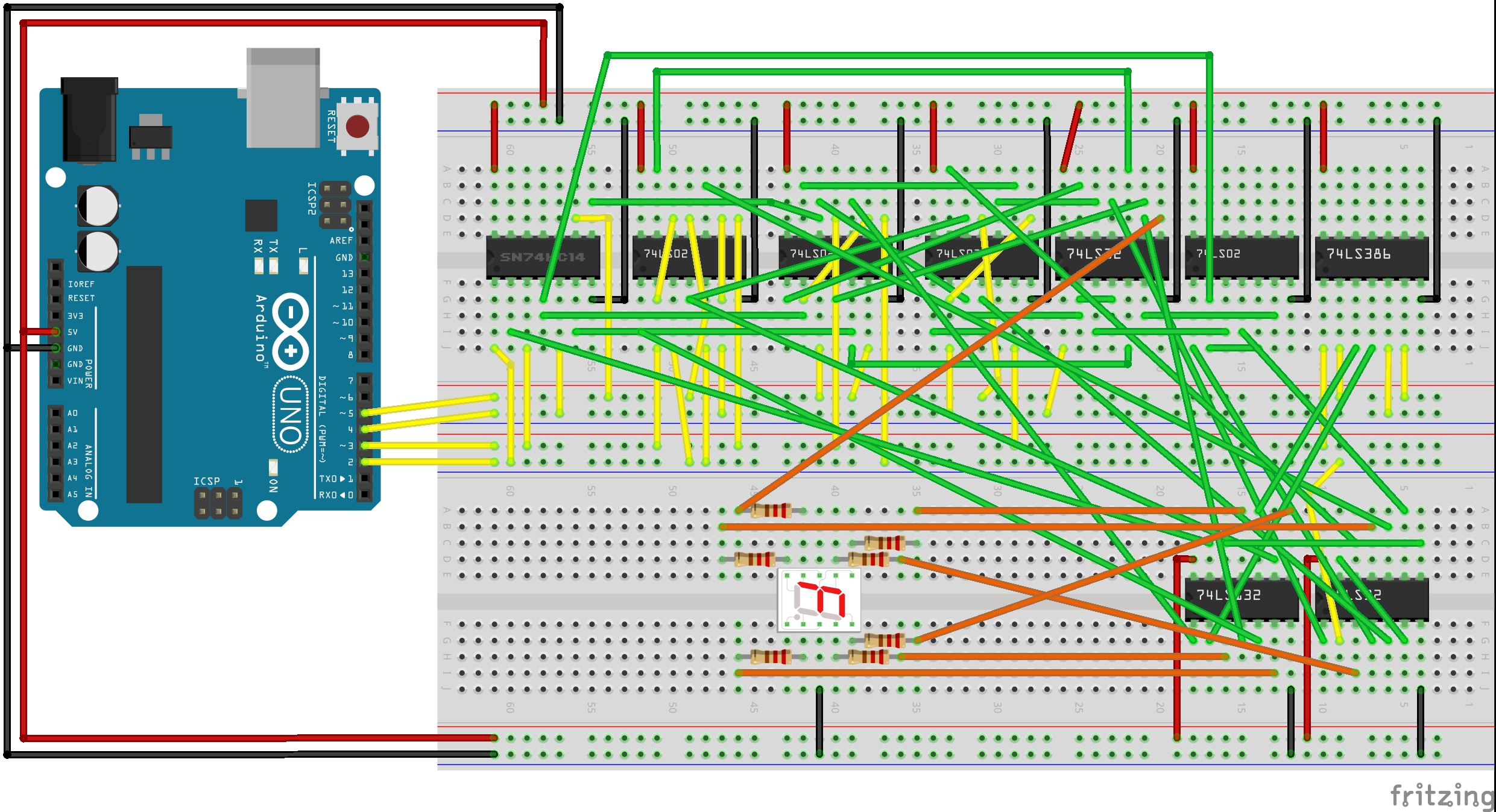
Driving it on the breadboard (manually pulling w,x,y,z high or low):

Driving it with an Arduino, see the CombinationalLogicDriver.ino sketch:

Credits and References
- Digital Logic & Computer Design - M. Morris Mano
- Boolean Algebra - wikipedia
- Combinational logic - wikipedia
- De Morgan’s laws - wikipedia
- Karnaugh Map - wikipedia
- Designing a 7-segment hex decoder - Ben Eater
- Building an 8-bit breadboard computer! - Ben Eater
- SC56-11 Datasheet - the common-cathode 7-segment LED display I’m using
- 74LS02 quad 2-input NOR gate datasheet
- 74LS14 hex Schmitt trigger inverter datasheet
- 74LS32 quad 2-input OR gate datasheet
- 74LS132 quad 2-input NAND Schmitt trigger datasheet
- 74LS136 Quadruple 2-input XOR with open-collector outputs datasheet
- 74LS386 Quadruple 2-input XOR datasheet
- ..as mentioned on my blog
