#389 Two-stage Common Emitter Amplifier

Designing a two-stage common-emitter BJT amplifier.

Build

Notes

Cascading two common-emitter amplifiers is a means of achieving high voltage gain. Voltage gains from several hundred to several thousand are possible.

I’m going to try and noodle out a theoretical design of a two-stage Class A amplifier, and then test the actual performance. Do not take my calculations as gospel. My main sources for the theory were Electronic Principles by Albert Paul Malvino and a Multistage Transistor Amplifiers YouTube tutorial by The Offset Volt:

Designing a Single Stage for Gain ~ 10

Parameter	Design/Spec Value
A (gain)	10
Vcc	9V
Icq	4mA
Vceq	4.5V
ß (hFE)	100 - 400
hie	1kΩ - 10kΩ
Vbe	0.7V
RL	2.2kΩ

Also:

r’e = hie/hFE = 10kΩ/400 = 25Ω

Calculate collector + emitter resistance for desired gain at the Q point

Rc + Re = (Vcc - Vceq) / Icq
Rc + Re = (9V - 4.5V)/4mA = 1.13kΩ
assuming A ≅ Rc/Re
Re = 1.13kΩ - Rc
Re = 1.13kΩ/11 =100Ω
Rc = 1.03kΩ, say 1kΩ

With the selected components, the theoretical gain is thus 10

Calculate the combined bias gang resistance

Base current at the q point

Ib = 4mA / 100 = 0.04mA

Assume current through the gang at 10 x Ib as a rule of thumb to ensure “stiff” biasing i.e. 0.4 mA

So combined resistance = 22.5kΩ

Calculate the resistance of R1 and R2 components of the bias gang

Lower resistor R2:

voltage = 0.7 + Ic x Re = 1.1V

therefore R2 = 2.75kΩ say 3kΩ (standard value)

and therefore R1 = 19.5kΩ say 20kΩ (standard value)

Measure Performance - Single Stage

single-stage-bb-test

With 0.2V peak-peak 10kHz input, and Re = 100Ω (without emitter bypass), measured results:

0.2V input peak-peak
1.98V output peak-peak
actual gain = 9.9

Conclusion: very close to design gain of 10, undistorted Class A performance.

single-stage-10kHz

Adjusting Single Stage Design with Bypass

I decided to add another 100Ω/100µF emitter bypass to the design, for a few reasons:

it’s a common feature of such designs
it provides negative feedback to stabilise for transistor variations (AC signals will vary the emitter resistance with inverse relationship to input/output differential, thus combating variation)
reduces the gain a bit (so I can work with larger input signals in two-stage configuration while staying within the 9V supply limits)

Recalculating with this variation. DC characteristics are now:

Re = 200Ω
A ≅ Rc/Re = 1kΩ/200Ω = 5

combined base bias resistance should still be = 22.5kΩ

Lower resistor R2 is now:

voltage = 0.7 + Ic x Re = 1.5V

therefore R2 = 3.75kΩ say 3.6kΩ (standard value)

and therefore R1 = 18.9kΩ say 20kΩ (standard value)

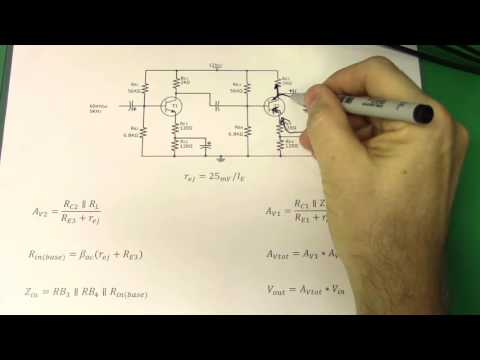
Calculating Two-stage Performance with RL load

With:

component values duplicated the from the single-stage design for two stages
with the extra 100Ω||100µF emitter bypass
and RL = 2.2kΩ

predicted performance calculated as follows:

DC analysis:

Vb = Vcc x Rb2/(Rb1 + Rb2) = 9V x 3.6kΩ/(20kΩ + 3.6kΩ) = 1.37V
Ve = Vb - 0.7V = 0.67V
Ie = Ve/Re = 0.67V/(200Ω) = 3.35mA
Ie ≅ Ic
Vrc = Ic x Rc = 3.35mA x 1kΩ = 3.35V
Vce = Vcc - (Vrc + Ve) = 9V - (3.35V + 0.67V) = 4.98V
Isat = Vcc/(Re + Rc) = 9V/(200Ω + 1kΩ) = 7.5mA

Second stage:

assuming thermal voltage VT = kT/q = 25 mV
r’ej = VT/Ie = 7.5Ω
A2 = Rc||RL/(Re2 + r'ej) = 1k||2.2kΩ/(100Ω + 7.5Ω) = 6.4
Rin(base) = ß(Re2 + r'ej) = 100(100Ω + 7.5Ω) = 10.75kΩ
Zin = Rin(base)||Rb1||Rb2 = 10.75kΩ||20kΩ||3.6kΩ = 2.38kΩ
A1 = Rc1||Zin/(Re1 + r'ej) = 1kΩ||2.38kΩ/(100Ω + 7.5Ω) = 6.55
Total gain A = A1 A2 = 6.4 6.55 = 41.92

Assuming headroom for say 7V peak-peak, input limit would be around 0.17V peak-peak before clipping.

Measure Performance - Two Stage

With 0.1V peak-peak 10kHz input, and Re = 200Ω (with 100Ω/100µF bypass), measured results:

0.1V input peak-peak
3.88V output peak-peak
actual gain = 38.8 = 31.8 dB
error in the theoretical gain calc = 7%

Conclusion: predicted performance was quite close to the actual performance. And .. I have a functioning two-stage Class A amplifier to boot, with performance “in the ballpark” of the design.

two-stage-10kHz